マイケル
みなさんこんにちは!
マイケルです!

エレキベア
こんにちクマ〜〜〜

マイケル
今回は久しぶりのp5.jsで学ぶゲーム数学シリーズ!
取り上げるのは「フーリエ解析」です!

エレキベア
フーリエ解析・・・
難しそうクマ〜〜

マイケル
フーリエ解析は 音の波形を周波数分解 するのによく使われる手法です!
実際に音を鳴らしながら感覚を掴んでいきますが、原理はシンプルで面白いのでお楽しみに!

エレキベア
サウンド分野で使える手法なのクマね

マイケル
なお、今回実際にプログラミングで使用されるFFT(高速フーリエ変換)については取り上げません!
原理が分かりやすいよう、数式ベースで実装しますのでご了承ください。。

エレキベア
FFTもまた別の記事で取り上げてくれクマ
参考書籍

マイケル
フーリエ解析の実装を行うにあたり、
下記書籍のフーリエ解析の章を参考にさせていただきました!


エレキベア
プログラミングで使う数学全般が載っているクマね

マイケル
そしてフーリエ解析自体については、下記のマンガでわかるシリーズから入りました!
何も知らない状態から学習する場合、ハードルが低いのでおすすめです!


エレキベア
流体力学あたりも面白かったクマね

マイケル
ちなみに今回様々な波形が登場しますが、こちらは下記のWebツールを使用しながら確認しました。
他にも類似のツールはあると思うので、ぜひ自身で関数を入力して確認しながら見てみると楽しめると思います!

エレキベア
数式だけみても中々イメージしにくいクマからね
フーリエ解析とは(理論)

マイケル
まずフーリエ解析とは何かというと、一般的な関数を三角関数の合計で表現・近似するための手法です。
よく使用される例としては、オーディオ波形から各周波数成分を求める 例があります。
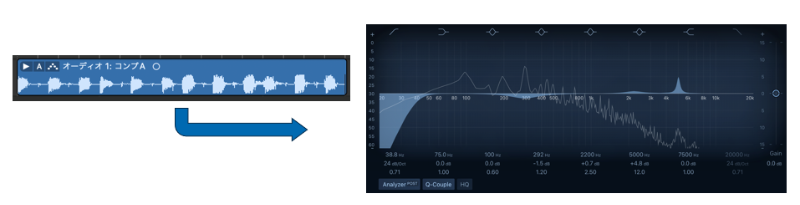
▲オーディオ波形から周波数を求める

エレキベア
周波数はイコライザで見れる成分になるクマね
どうやって求めるかなんて、想像もつかないクマ

マイケル
この波形だけみると、そんなことほんとにできるの?って思うよね・・・
フーリエ解析の説明に入る前に、まずは音の波形の基本構造を見てみましょう!
sin波とcos波

マイケル
三角関数のsin、cosは覚えていますでしょうか?
なんとこのsin関数で作られた下記の式が音の最も基本的な波形として定義されています。

マイケル
純音やシヌソイド関数とも呼ばれていて、fは周波数(1秒に振動する回数)です。
fの値を大きくするとその分振動数が増え、音も高くなります。
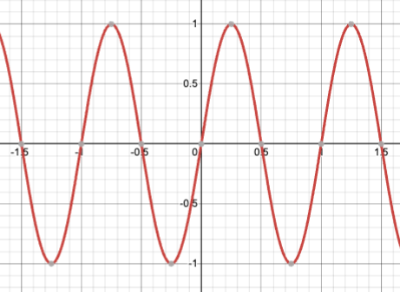
▲sin2πtの関数
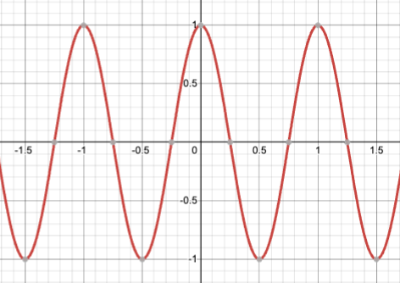
▲cos2πtの関数

エレキベア
sin、cosは波のように繰り返す性質があったクマね
これが音の波形の基本なのクマか・・・

マイケル
そして音の大きさは振幅(振動の大きさ)、音の高さは周波数で決まっていて、振動が大きくなるほど音も大きく、振動する回数が多くなるほど音も高くなります。
例えばラ(A)の高さだと441Hzと決められています。

エレキベア
振動数と大きさで音の高さ・大きさが分かるクマね

マイケル
ちなみにsin波以外でよく使われる波形についても下記に記載してあります。
興味がある方はよければご参照ください!
【ソフトシンセ】シンセサイザ を使って効果音を一から作成する
2020-05-31

エレキベア
シンセで音作りする時にも使うクマね
フーリエ級数

マイケル
音の高さと大きさは周波数・振幅で決まりますが、
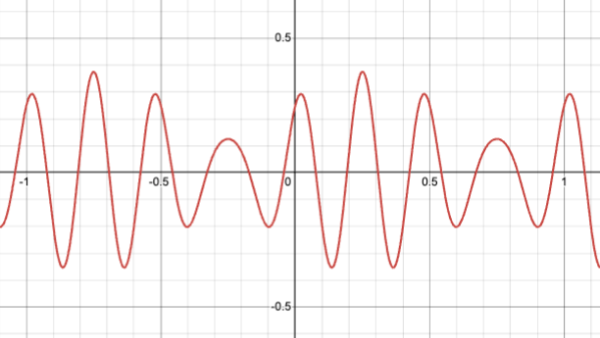
実際の音の波形は複雑で、これが音色に値します。

エレキベア
うーむ・・・
ワケが分からんクマ・・・

マイケル
このような、どんな複雑な波形でも全ての波形はcos、sinの組み合わせで表現できる という定理が フーリエ級数 になります!
▲フーリエ級数の式(※a0/2:n=0のcosの係数は2a0のため)

エレキベア
cosとsinの組み合わせで・・・表現できる・・・?

マイケル
混乱しているようだね・・・
例をあげると、先ほど示した波形も下記のように単純なcos、sinの波形に分解できる、ということになります。
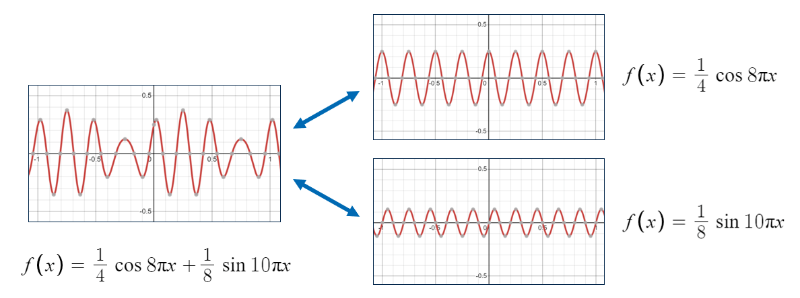
▲複雑な波形もcos、sinの組み合わせの式で表現することができる

エレキベア
ほうぅクマ・・・
信じがたいクマが中々面白い定理クマね
フーリエ解析

マイケル
ここでもう一度フーリエ級数の式を見てみます。
最初の話を思い出すと、この式でいうan、bnが振幅、nが周波数ということになります。

エレキベア
ということは・・・

マイケル
この係数を求めることができれば、周波数成分を抽出することができるということです!

エレキベア
きたクマ〜〜〜
イコライザへの道が一歩開けたクマ

マイケル
問題はこの係数をどうやって求めるか?ですが、これには関数の直行性を利用します。
関数の直行とは違いに交わらない関数同士を指し、2つの関数を掛け合わせて定積分した結果が0になるといった特徴があります。

エレキベア
それと今回の式とどう関係があるクマ??

マイケル
実はcosnx、sinnxといった周期の異なる関数は全て直行している状態になります。
つまり、それぞれの関数で積分することでその関数のみが残り係数部分を求めることができるというわけです!
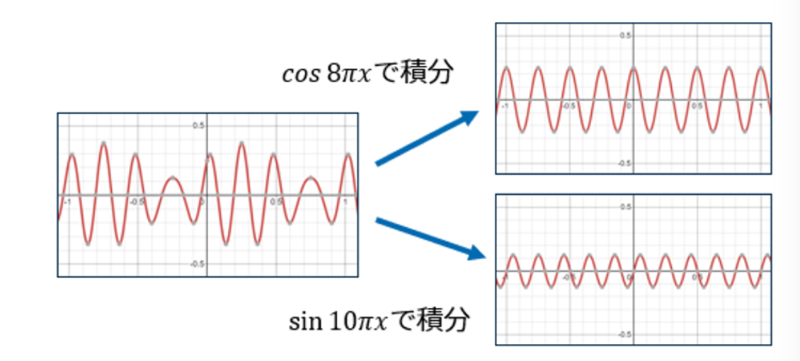
▲それぞれの関数で積分することで周波数成分を抽出することができる

エレキベア
そういうことクマか・・・!!

マイケル
これを式で表すと下記のようになります。
▲各成分の計算

エレキベア
関数に求めたい周期の関数を掛け合わせたものを0-2πの間で積分するクマね

マイケル
この「1/π」がどこからきているのかというと、最終的に残った「sin^2」「cos^2」を積分した結果(面積)がπになるため、最後に割ることで係数部分を求めているというわけです。

エレキベア
これで係数はばっちり求められそうクマね

マイケル
最後に、求めたいのは周波数成分になるため、sin、cosでそれぞれ同じ周波数の成分をベクトルの長さとして考えて計算することで求めることができます。
以上でフーリエ解析の説明は完了です!!
▲最終的な周波数成分の計算

エレキベア
フーリエ解析すごいクマ〜〜〜
波形によるサウンド再生

マイケル
フーリエ解析の概要が分かったところで、ここからは実際にコードを書きながら波形を再生していきましょう!
まずは波形・・・といっていいかは分かりませんが、ランダムに生成したノイズ波形の再生を行ってみます。
時間を引数にとって波形を生成する関数は下記のようになります。
▲ノイズ波形の関数

エレキベア
ほんとにぐちゃぐちゃした波形ができそうマね

マイケル
この関数を使用してWebで音を鳴らす方法として、AudioBufferを使用しました。
関数を受け取って再生する処理は下記のようになります。
サンプルレート分配列を用意してそちらに関数から得られたデータを格納しています。
参考:
BaseAudioContext.createBuffer() - Web API | MDN
▲波形関数からのサウンド再生

エレキベア
Webでも波形データから再生することができるのクマね

マイケル
これらを使用して音声を再生したサンプルが下記になります!
ボタン押下することで音声が再生され、波形も表示されるようにしています。
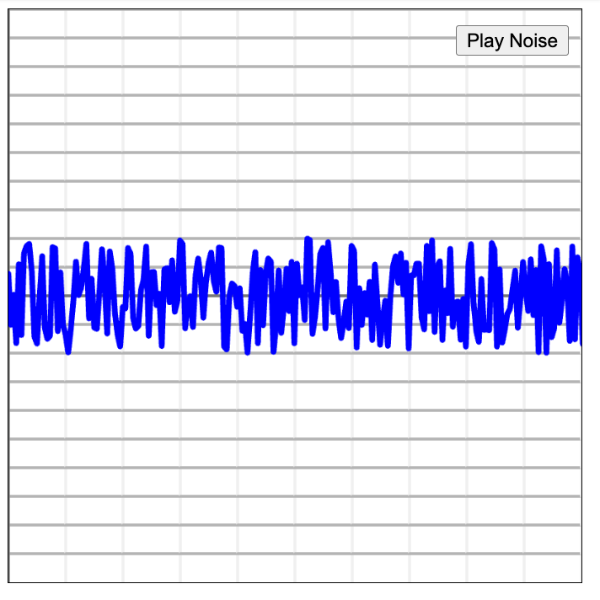
▲ノイズ波形の表示

エレキベア
おお〜〜〜
このよく聞く音はノイズ波形だったのクマね

マイケル
不規則な波形にするだけでこんな音が作れるのは面白いよね!
次は最初に解説したsin、cos波形を再生してみます。
こちらの関数と再生サンプルは下記になります。
▲sin、cos波形の作成
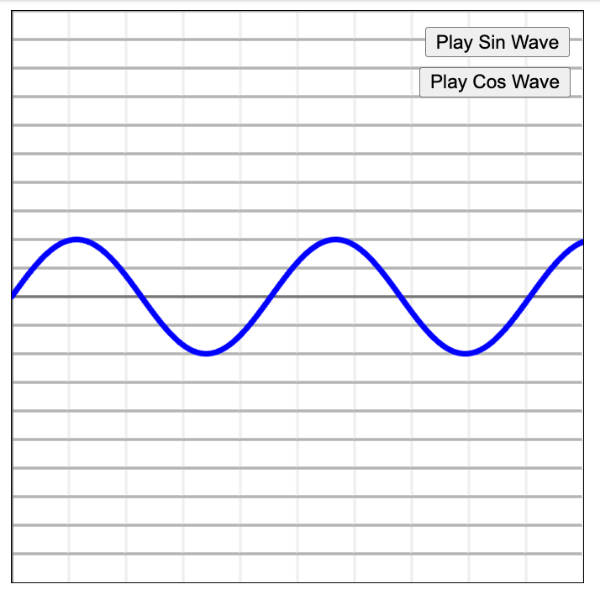
▲sin波形の表示
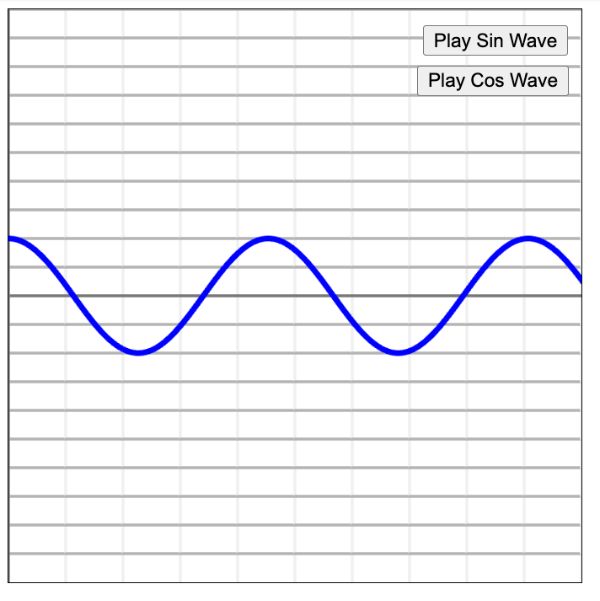
▲cos波形の表示

エレキベア
基本的な波形という情報を聞いていたこともあってか、
シンプルな音に聞こえるクマ
シンプルな音に聞こえるクマ

マイケル
cos波形はsin波形がずれただけだから、音色としてもほぼ変わってないね
フーリエ級数による波形作成

マイケル
それでは次はフーリエ級数を使用して作成した波形で音を鳴らしてみます。
復習になりますが、フーリエ級数は下記のような式になっていました。

マイケル
これを関数に落とし込むと下記のようになります。
サウンド再生で確認しやすいよう、ベースとなる周波数も指定できるようにしてあります。
▲フーリエ級数による波形関数

エレキベア
anとbnの配列を渡すことで作成しているクマね

マイケル
この関数を使用して何種類か波形を作成して再生するサンプルは下記になります。
▲フーリエ級数による波形の作成例
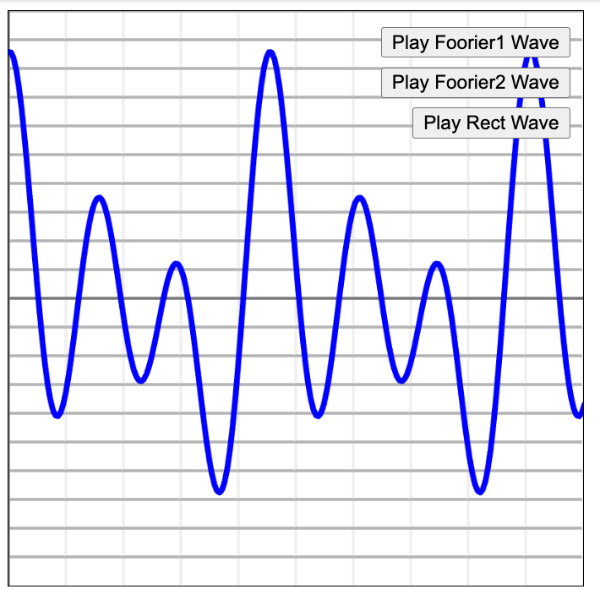
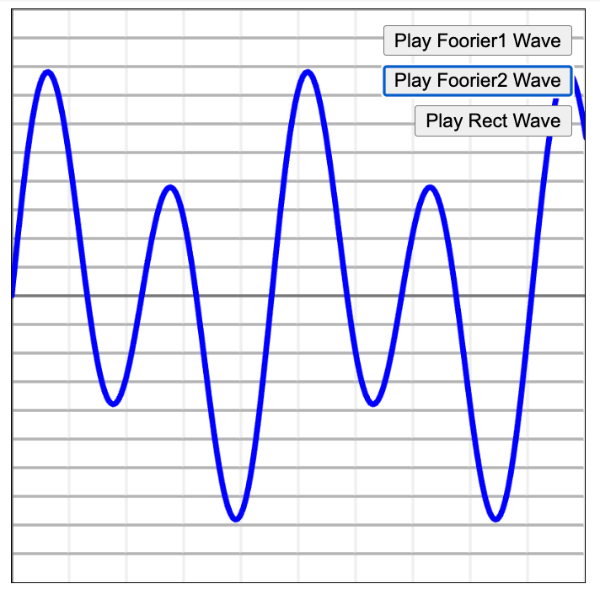
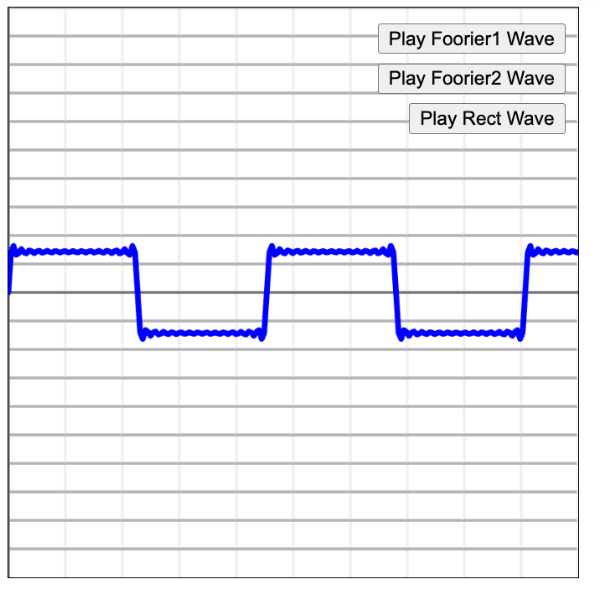

エレキベア
いろんな形状の波形が作成できるのも、それで音色が変わるのも面白いクマね〜〜

マイケル
最後のは短形波といって、こんな波形もsin、cosの組み合わせで表現できてしまいます。
bCount変数を増やすことでより短形波に近づくので、値を変えて試してみてください!
フーリエ解析

マイケル
最後に波形関数から作成したデータから、フーリエ解析で元の係数を求めてみます。
係数an、bnを求める式は下記になっていました。

エレキベア
関数同士を掛け合わせたものを積分して求めるのだったクマね

マイケル
これを計算しやすいよう、0-1の範囲で書きなおすと下記のようになります。
今回はこちらの式を使用して実装しました。
▲フーリエ解析関数

エレキベア
係数を求めて返却する関数クマね

マイケル
この関数を使用して、サウンド再生後に係数を求めて表示する処理とサンプルは下記になります。
▲フーリエ解析の実行
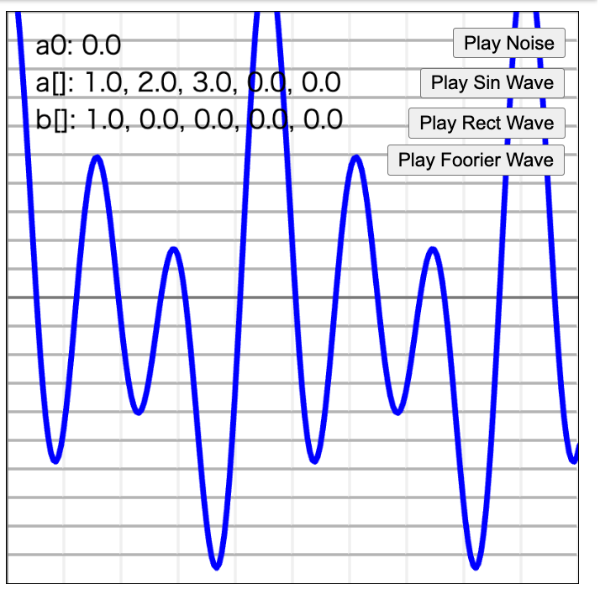
▲フーリエ解析の例

エレキベア
ちゃんと求められてるクマ〜〜〜

マイケル
これで当初の目的だった、「波形データから周波数成分を求める」という目的が達成できました!
おわりに

マイケル
というわけで、今回はフーリエ解析についてでした!
どうだったかな?

エレキベア
波形から周波数成分を求めるなんて最初は予想も出来なかったクマが、
原理が知れて楽しかったクマ〜〜〜

マイケル
実際にサウンドと波形を確認しながら見るのは中々面白かったね!
これを実際にゲーム等で使用する場合には、処理を高速化したFFT(高速フーリエ変換)という手法があります。
FFTを使用してUnityでオーディオスペクトラムを実装した例もありますので、こちらもよければご参照ください!

【Unity】第三回 UnityAudioを使いこなす 〜オーディオスペクトラム描画編〜
2024-01-22

エレキベア
Unity含めてFFTライブラリはよく用意されているクマね

マイケル
それでは今日はこの辺で!
アデューー!!

エレキベア
クマ〜〜〜〜
【ゲーム数学】第九回 p5.jsで学ぶゲーム数学「フーリエ解析」〜完〜